DSA 笔记 -> Heap

Heap and Heapsort

(部分内容使用ChatGPT 5.1生成)

Heap（堆）是什么？

Heap 是一种特殊的“几乎完全满”的二叉树（almost perfect binary tree）。
它不仅结构特别，而且还满足一个很重要的性质：堆序性（heap order property）。

Heap 的两个核心特性

1. 结构性质：完全二叉树
   也被叫做 binary heap，要求：

• 除了最底层，其他每一层都是满的
• 最底层如果不满，必须从左往右依次填满
• 没有缺口（holes）

这使得 堆非常适合用数组实现，因为它的形状很规则。

举例：
对数组中下标为 i 的节点：

• 左孩子在 2*i + 1
• 右孩子在 2*i + 2
• 父节点在 (i−1)/2

holes 的意思：

对于完全二叉树，每一层的节点数是2的层数-1(n-1)次方。

• 第一层 2^(1-1) = 1
• 第二层 2^(2-1) = 2
• 第三层 2^(3-1) = 4

2. 堆序性：父节点必须小于或等于子节点（最小堆）
   子节点的数值必须大于父节点的数值，这样的最小值永远在根节点（顶端）。

insert()

insert(x)
1. IF ISFULL(A)
2.       return False // 检查是不是满了，插不进去了
3.   // percolate up
4.   hole = size++ // 在末尾挖一个洞，先赋值再自增
5.   WHILE hole > 0 AND x < A[(hole-1)/2]
            // hole = 0，到根了不能上升
            // x < A[(hole-1)/2]子节点小于父节点，交换父节点和hole
6.         A[hole] = A[(hole-1)/2]
           hole = (hole-1)/2
7.   A[hole] = x
8.   return True

解释关键变量：

• hole：当前“洞”的位置（用来“挖坑”往上走）

• size++：插入前堆有 size 个元素，新元素先占用 A[size] 位置，size 再加 1

不用担心，因为既然hole能到这个位置，那么之前的数据都窜下去了，给父节点赋到子节点不会丢失内容。

deleteMin()

deleteMin()
1. IF ISEMPTY(A)
2.       return -1 // 空了不能删
3.   min = A[0], hole = 0, x = A[--size]
    // 删掉的最小值要返回，然后给hole设成这个位置，移动hole
    // size-1是最后一个元素的下标，x = 最后一个元素的值
4.   // percolate down
5.   WHILE A[hole] has children
        // 用2*hole+1和size比较
        // 注意如果2*hole+2没有东西了的情况，sid直接为2*hole+1
6.        sid = index of A[hole]’s smaller child
7.        IF x <= A[sid]
8.              BREAK
        // 如果hole往下降到正确的位置，停止下降
9.        A[hole] = A[sid]
10.       hole = sid
11.  A[hole] = x
12.  return min

关键变量解释：
sid: 实际上循环是 while ((2*hole+1) < size)

if ((2*hole+2) >= size) {
    bid = 2*hole+1; // Only left child exists
} else {
    bid = (A[2*hole+1] < A[2*hole+2] ? (2*hole+1) : (2*hole+2)); // Select smaller child
}

heapSort()

我们不需要多余的空间来进行排序，一个数组中：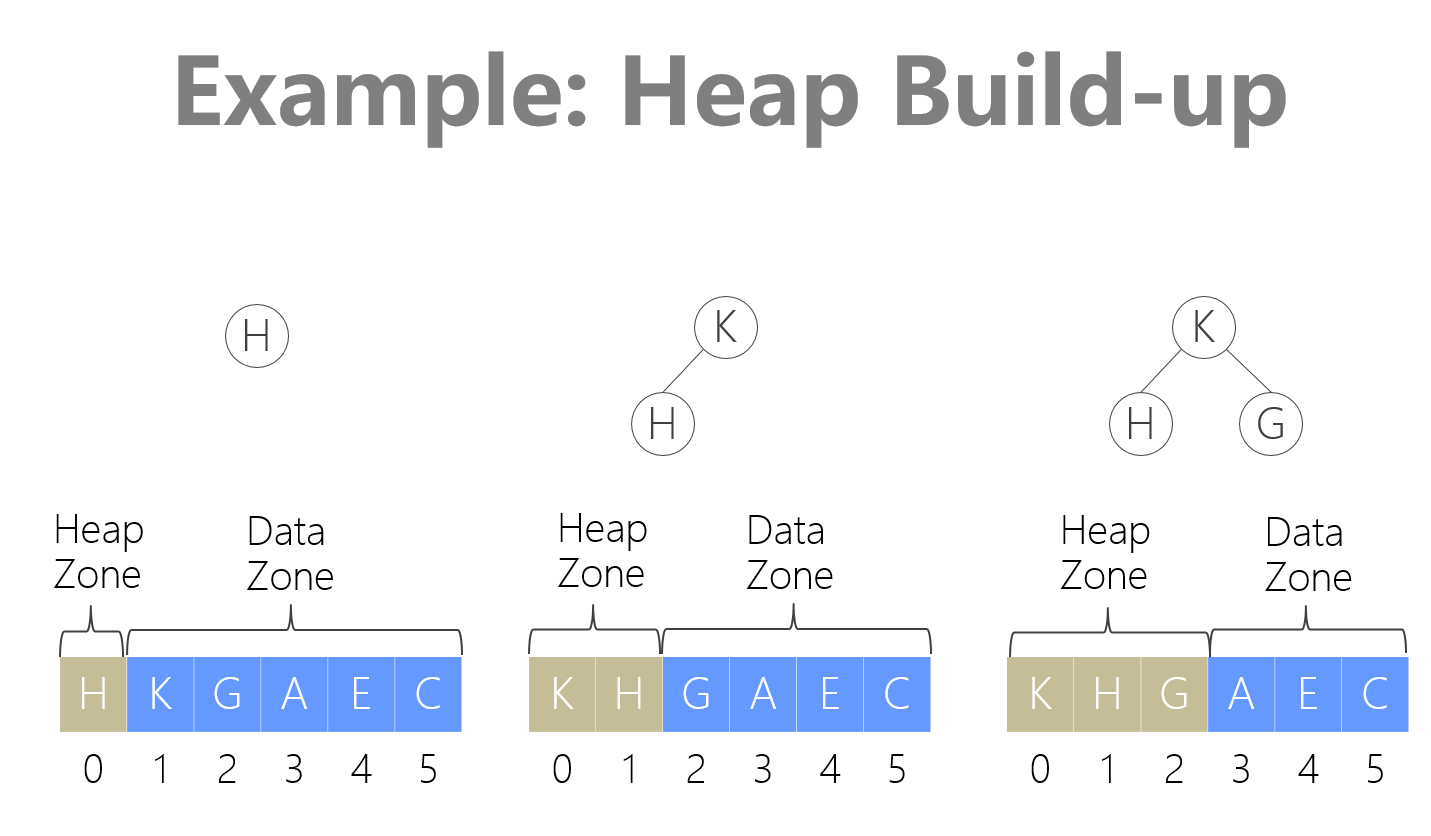

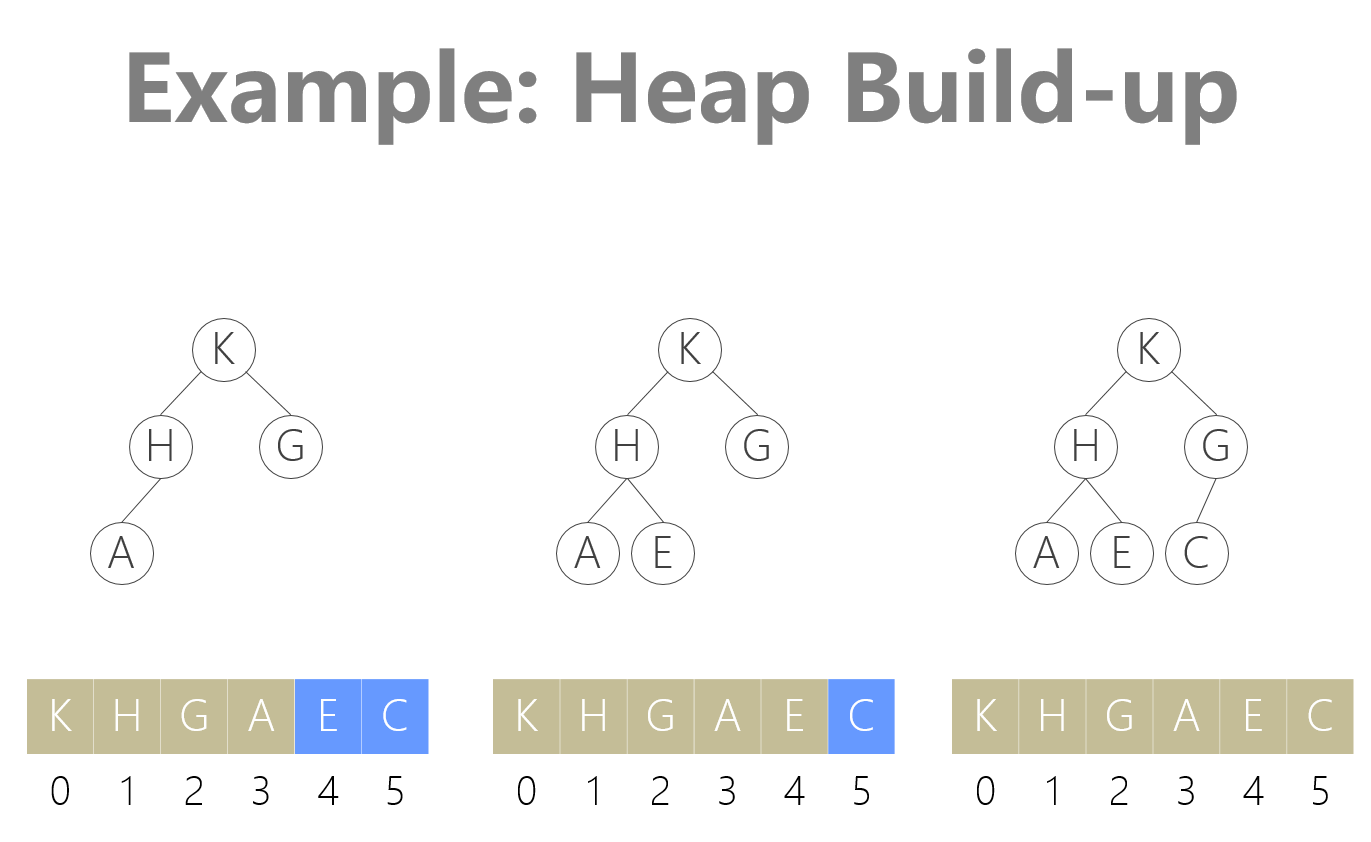
直接给他们归成MaxHeap的形式，来存档。

MaxHeap就是给MinHeap反过来。insert的过程，将第5步的<换为>即可。deleteMin换为deleteMax，然后更换sid为bid，就是给bid赋值过程的判断反向，BREAK也换为>=。

存进去，倒着deleteMax出来，……

public static void heapSort(int A[]) {
	MaxHeap heap = new MaxHeap(A); // Heap backed by same array
	for (int x : A) {
		heap.insert(x); // Build heap one value at a time
	}
	for (int i = (heap.size - 1); i > 0; i--) {
		A[i] = heap.deleteMax(); // Pull max into sorted suffix
    }
}